Defining Optimization in Machine Learning

Optimization is an elegant term that, in simple words, means finding the ideal method of doing something. Or deciding on the best way, if you will. Choosing the right clothing size, following the most efficient route to your destination, or finding the ideal water temperature after a long agony while taking a shower… These are all examples of how this concept works. And once you’ve found the most optimal value, you stick to it from now on.

In machine learning, optimization is a little more complicated. To give you an idea, when we talked about choosing the most comfortable water temperature in the shower, ML specialists would call it gradient descent. When you go through lots of stores in the shopping mall to find the best-suited dress or a pair of jeans, we call it an exhaustive search in machine learning, another example of an optimization method.

So far, these are all obscure terms to you. We’ll fix that very soon, but let’s start with the basics. The main task in machine learning is to create a model that demonstrates excellent performance and generates accurate predictions or recommendations in a given set of scenarios. ML optimization is necessary for achieving it. In fact, an optimization method is operating in the background as we train a machine learning model.

So, how do we define machine learning optimization? Do we really need it?

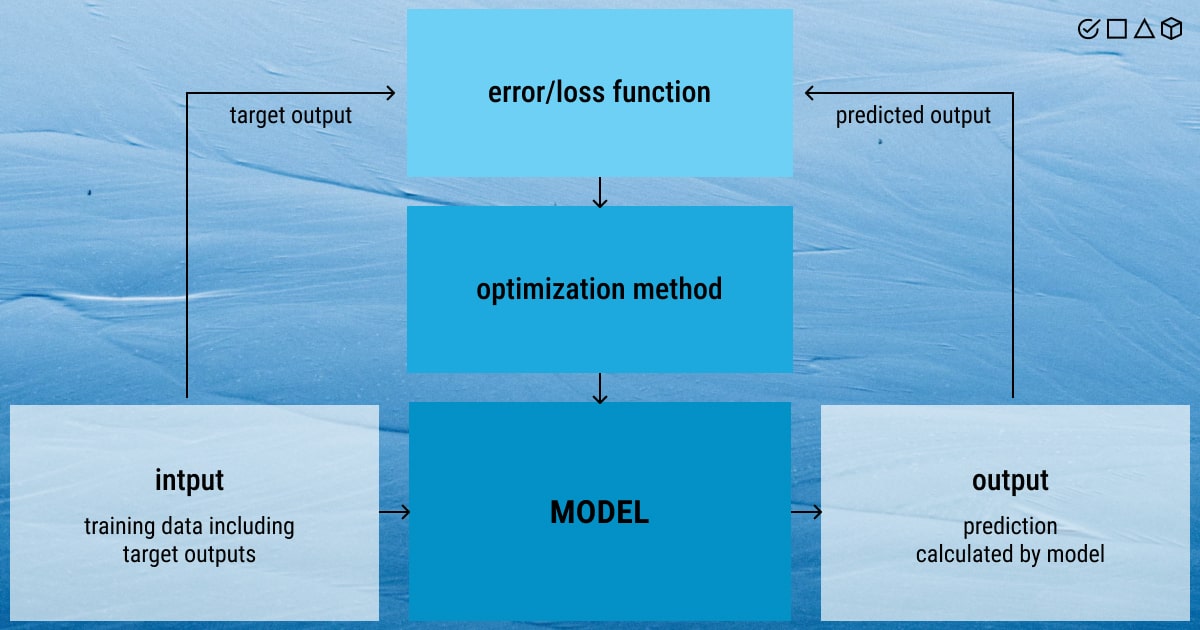
The process of machine learning optimization entails modifying the hyperparameters in order to use one of the optimization approaches to reduce the cost function. Because the cost function explains the difference between the estimated parameter’s real value and the model’s prediction, it is crucial to minimize it.

Central to machine learning is function optimization. The reason for this is that all ML algorithms use function optimization to adjust a model to a training dataset. For example, you need to fit a linear regression or a neural network model on a training dataset. In this case, optimization serves as a viable asset to modify a general model to suit a particular scenario.

With this in mind, we can sum up that a family of issues known as function optimization is concerned with determining the input to a particular function that will produce the function’s minimum or maximum output. Three factors are necessary for function optimization:

• Input to the function: A candidate solution.
• Objective function: A target function that evaluates inputs (i.e., candidate solution).
• Output from the function: The results of the evaluation process (i.e., evaluation costs).

However, function optimization can get tricky, given that there may be hundreds and thousands, or even millions of inputs. Plus, the structure of the function is unidentified, and it’s often non-differentiable and noisy.

Continuous function optimization is the most prevalent category of optimization issues in machine learning. To solve such optimization problems, there is a wide variety of optimization algorithms that may be utilized, as well as possibly an equal number of grouping and synthesis techniques. Learn more about this algorithm optimization, the most frequent optimization issues in machine learning, and methods for resolving them by reading on!

Why Do We Need Optimization for Machine Learning?

We already know that in supervised learning, ML models require labeled training data to learn the correlation between input and output variables. After that, a model can perform a wide range of tasks in machine learning, like recognizing patterns in data, making predictions about trends, or classifying new input data. A model training is the optimization process itself, with each iteration aiming to increase the model's precision and decrease its error margin.

Repeatedly boosting an ML model's accuracy while reducing its level of error is called machine learning optimization. The insights gained from training data are used by these models to generalize and predict outcomes for fresh live data. In practice, this is executed by roughly simulating the underlying function or relationship between the input and output data. Minimizing the difference in output between the expected and actual results is a key objective of training a machine learning system.

The importance of machine learning optimization knows no limits. Why is that so?

Every stage of ML revolves around optimization. This comprises a data scientist improving and tweaking labeled training data or training and enhancing models iteratively. An ML model is then trained to execute a function in the most efficient manner, which is fundamentally an optimization concern. The fine-tuning and adjustment of model settings or hyperparameters is the most significant aspect of ML optimization.

What are these hyperparameters? The components of the model that the data scientist or developer has established are known as hyperparameters. Hyperparameters may contain characteristics like the model’s structure, learning rate, or the amount of clusters used to categorize data. It’s a method of improving a model to match a particular dataset and comprises components like the learning rate or the number of classification clusters.

The model, however, doesn’t create hyperparameters from training data. To properly accomplish the unique goal of the model, they must be tweaked. Conversely, the machine learning model itself develops other parameters during training (e.g., data weighting). An accurate and effective machine learning model depends on choosing the best hyperparameters. To create the most accurate model, it is crucial to optimize the hyperparameters. The procedure might be referred to as hyperparameter optimization or tuning. Because maximum precision, efficiency, and few mistakes are the main goals we pursue in machine learning.

What Is Model Optimization?

How do you measure optimization in machine learning? A loss or cost function, which generally defines the difference between the expected and actual value of data, is used to quantify optimization. The goal of machine learning models is to minimize this loss function or to narrow the discrepancy between output data predictions and reality. The ML model will improve in accuracy when predicting an outcome or classifying data through iterative optimization.

Cleaning and preparing training data may be thought of as a phase in the optimization of the machine learning process. To enable a machine learning model to be used, raw, unlabeled data must be turned into training data. We all know very well that this is possible with quality data annotation. Discover the potential of labeled data for your ML project with experts in the field, like we are at Label Your Data! Send your data to us, and we’ll provide you with a free pilot, fully customized to your specific requirements!

Yet, the iterative improvement of model settings known as hyperparameters is often what is regarded as machine learning optimization.

Now, if your model functions well, it’s exactly the right time to optimize its quality. Optimization techniques for ML models are less complicated compared to those mathematically-driven algorithms used for other tasks in machine learning (that we’ll discuss shortly).

Here are the steps required for ML model optimization:

1. Include useful features

   By adding features that encode data that your present features are unable to, you can increase model performance. Using correlation matrices, you may identify linear relationships between certain attributes and labels. You must train the model with and without the feature, or a mix of features, and look for an improvement in model quality to find nonlinear correlations between features and labels.

2. Hyperparameters tuning

   Even if you discovered the values of the hyperparameters required to run your model, they still need to be adjusted. The settings may be manually adjusted by trial and error, but this takes a lot of time. Instead, think about employing a service for automated hyperparameter tuning. This is how you deploy artificial intelligence in ML optimization.

3. Work with depth and width

   These hyperparameters were only enhanced during the debugging process. Yet, depending on your objectives, you either increase or reduce depth and width during model optimization. Try lowering overfitting and training time by reducing depth and breadth if your model quality is sufficient. You must strike a balance between quality, overfitting, and training duration since your model quality will also decline.

Overview of the Main Optimization Issues in Machine Learning

Many machine learning models rely on mathematical programming as a core component, and training these models is an enormous optimization issue. Regression, classification, clustering, deep learning, as well as the newly developing concepts of machine learning and empirical model learning, will be discussed below.

Let’s review the distinguishing characteristics and potential unsolved machine learning issues that might be helped by developments in computational optimization.

• Regression. Shrinkage techniques and dimension reduction are common strategies to prevent overfitting and manage data uncertainty. These strategies may all be described as models for mathematical programming. It is still computationally difficult to solve to optimality general non-convex regularization to guarantee sparsity without introducing shrinkage and bias.
• Classification. Classification problems are optimization problems as well. Classifier sparsity, like in regression, is a crucial strategy to prevent overfitting. Furthermore, since nonlinear separators may be generated with minimal added complexity, leveraging kernel methods is essential. Making use of kernel techniques in sparse SVM optimization models is still a mystery when presented as an optimization issue. The optimization literature has extensively studied the topic of handling data uncertainty through robust and stochastic optimization.
• Clustering. In general, mixed-integer nonlinear programs (MINLPs) are used to describe clustering issues that are complex to find an optimal solution for. Handling non-convexity and large-scale instances is one of the difficulties, which is difficult even for linear variations like capacitated centered clustering (formulated as a binary linear model). Heuristics are generally developed, particularly for large-scale scenarios.
• Deep Neural Networks (DNNs) architecture. Due to the magnitude of the underlying optimization model, the benefit of mathematical programming techniques for modeling DNNs has only been demonstrated for very modest data sets. Additionally, addressing the uncertainty in the training data and defining misclassification requirements for adversarial cases are unresolved issues in this case.
• Adversarial learning and robustness. To find new sets of attacks and then defend against them, optimization models for the search for adversarial instances are essential. Here, the classifier function has a significant impact on how sophisticated the mathematical models are. Designing models that are resistant to adversarial attacks is also a two-player game that may be framed as a bilevel optimization issue. The mathematical model that results has some primary complexity due to the loss function that the learner chose, and different techniques to solve the problem still need to be researched.
• Data poisoning. This is an adversarial attack that affects a training dataset, causing the algorithm to classify bad instances into the desired classes. It’s a game for two when it comes to protecting against the poisoning of the training data. Since the KKT (Karush-Kuhn-Tucker) criteria do not apply, the issue of online data retrieval presents particular difficulties for gradient-based algorithms.
• Activation ensembles. The accuracy of the classifier and the computational ease of training using a mathematical programming technique are trade-offs sought after by activation ensembles. However, large DNNs being trained using activation ensembles have not yet been researched.
• Machine teaching. The development of computationally tractable single-level formulations that model the learner, the teaching risk, and the teaching cost is one of the issues in machine learning. Machine teaching is considered a bilevel optimization problem. Several two-player games, such as data tampering and adversarial training, which are significant in practice are also generalized by machine learning.
• Empirical model training. This new paradigm may be thought of as the link connecting operations research for optimization with machine learning for parameter estimation. Thus, there are still certain theoretical and practical issues to be looked at before suggesting prescriptive analytics models that simultaneously combine learning and optimization in real-world applications.

A Comparison of Machine Learning Optimization Algorithms

Optimization algorithms, which employ a variety of methods to hone and enhance the model, may carry out machine learning optimization.

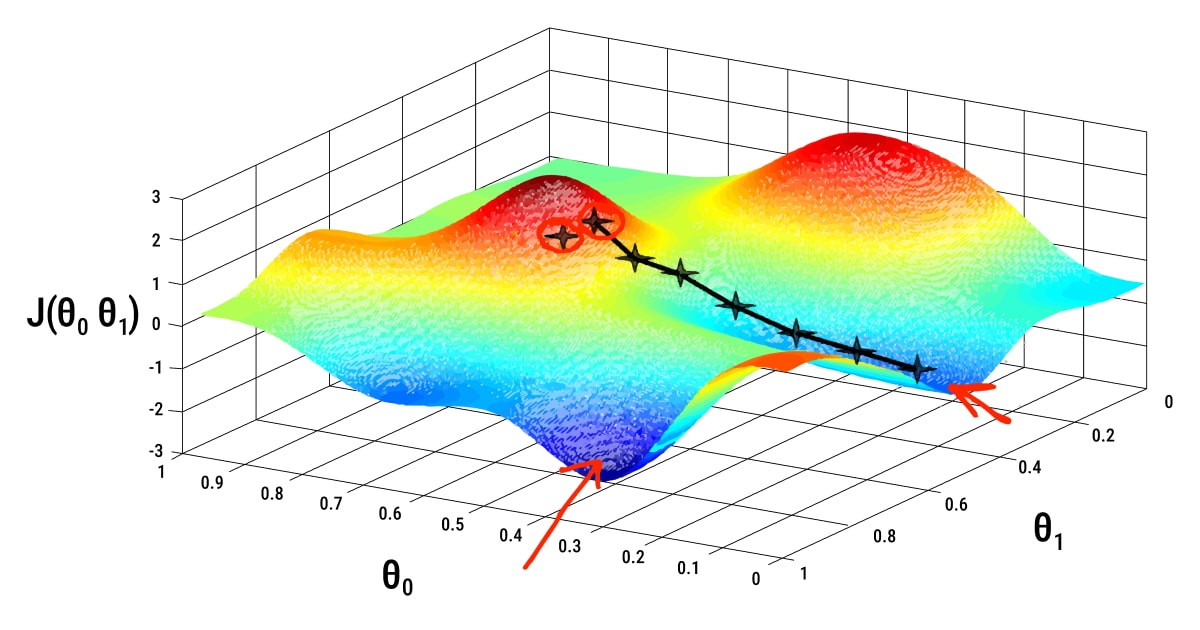
Whether or not the objective function (mentioned before) can be distinguished at a certain moment is maybe the key distinction between optimization techniques. In other words, if a certain candidate solution can be used to determine the function's first derivative (gradient or slope). This separates algorithms into those that can use the computed gradient information and those that cannot.

In this article, we’ll take a look at algorithms for differentiable (make use of derived data) and non-differentiable (don't make use of derived data) objective functions. They can be seen as the primary means of classifying the main optimization algorithms in ML.

Differentiable Objective Function

• Bracketing Algorithms: Fibonacci Search, Golden Section Search, Bisection Method.
• Local Descent Algorithms: Line Search.
• First-Order Algorithms: Gradient Descent, Momentum, AdaGrad, bRMSProp, Adam.
• Gradient Descent: Stochastic Gradient Descent, Batch Gradient Descent, Mini-Batch Gradient Descent.
• Second-Order Algorithms: Newton’s Method, Secant Method, Quasi-Newton Method.

Non-Differential Objective Function

• Direct Search Algorithms: Cyclic Coordinate Search, Powell’s Method. Hooke-Jeeves Method. Nelder-Mead Simplex Search.
• Stochastic Algorithms: Simulated Annealing, Evolution Strategy, Cross-Entropy Method.
• Population Algorithms: Genetic Algorithm, Differential Evolution, Particle Swarm Optimization.

Although we’ve covered the most important techniques you're likely to come across in machine learning, this isn't a full review of algorithms for continuous function optimization. Still, let’s review some of the above-mentioned optimization algorithms for machine learning.

Gradient Descent

The first and most widely used optimization technique is gradient descent. The fundamental principle behind this optimization approach is that variables should iteratively update in the opposite direction as the gradients of the objective function. A steady convergence to the objective function's ideal value is achieved by the update.

Stochastic Gradient Descent

Stochastic gradient descent’s main principle is to update the gradient by selecting a sample at random for each iteration, rather than computing the gradient’s precise value. The stochastic gradient is considered an unbiased estimation of the true gradient.

Adam

This optimization technique results in a rather steady gradient descent process. It works well for the majority of non-convex optimization issues involving sizable data sets and high spatial dimensions. But sometimes the approach might not converge.

AdaGrad

This method works well for solving issues with sparse gradients. Each parameter’s learning rate is adaptively adjusted. As training time is extended, the cumulative gradient will get steadily bigger, causing the learning rate to trend toward zero and leading to inefficient parameter updates. Still, a manual learning rate is required.

Newton’s Method

The Newton optimization technique employs second-order gradient information, which converges much faster than the first-order gradient method. In some cases, Newton’s method has quadratic convergence. However, the inverse matrix must be calculated and stored at each iteration, which takes a lot of time and storage space.

Summary: Back to the Question of Importance of ML Optimization

Optimization and machine learning is a match made in heaven, or rather in the world where the power of AI is becoming more and more tangible.

ML models are fundamentally based on optimization, with algorithms trained to carry out tasks in the most efficient manner. Whether classifying an object or predicting trends and patterns, machine learning models are used to anticipate the results of a function. The goal is to develop the most accurate model possible that can accurately translate inputs into expected outcomes.

As you’ve learned by now, the goal of ML optimization is to increase the model’s precision while reducing the likelihood of mistakes or losses resulting from these predictions. With that said, optimization makes AI a technology that we can trust. But never forget what brings trust to AI, and always feed your model with high-quality annotated data that our Label Your Data can provide and tailor specifically for your AI project!

Written by

Yuliia Kniazieva Editor-at-Large

One of the technical writers at Label Your Data, Yuliia has been gradually delving into the intricate aspects of AI. With her strong passion for the written word and technical expertise, Yuliia has developed a keen interest in the evolving field of data annotation and the power of machine learning in today's tech-savvy world. Check out her articles to learn more about the complex world of technology and find the solutions that work best for your AI project!